In [ ]:
from IPython.core.display import HTML

def _set_css_style(css_file_path):
   """
   Read the custom CSS file and load it into Jupyter.
   Pass the file path to the CSS file.
   """

   styles = open(css_file_path, "r").read()
   s = '<style>%s</style>' % styles     
   return HTML(s)

_set_css_style('rise.css')

numpy: arrays and functions¶

print view
notebook

  • numpy arrays
  • Math with arrays
  • More advanced slicing
  • Array views vs. copies
  • Reading in data with numpy

Arrays¶

numpy arrays are dense, continuous, uniformly sized blocks of identically typed data values

In [ ]:
import numpy as np
L = [[0,1],[2,3]]
A = np.array(L)
In [ ]:
print("L:",L)
print("A:\n",A)
In [ ]:
print(type(L),type(A))

Array memory layout¶

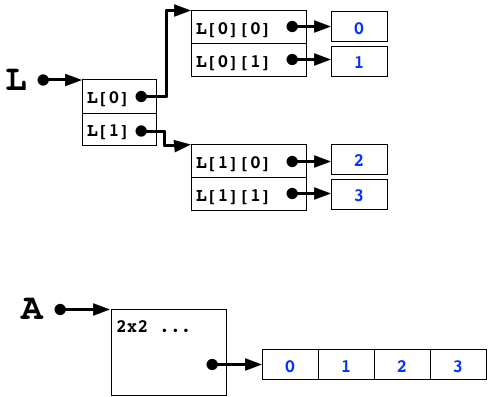
memory array

Array memory¶

In the standard python interpretter, the return value of id is the memory address of the object.

In [ ]:
print(id(L))
In [ ]:
print(id(L[1])-id(L[0])) # rows are far away
In [ ]:
print(id(L[0][1])-id(L[0][0])) # columns not so much

Why does this matter?¶

Keeping data close together results in faster access times.

  • It's easier to figure out the location of the data
  • The data is more likely to fit in the processor's cache

If you have a block of dense numerical data, store it in a numpy array

Creating numpy arrays¶

Note that np.ndarray and np.array are the same thing.

In [ ]:
A = np.array([1,2,3,4])
A.dtype # type of what is stored in the array - NOT python types!
In [ ]:
A.ndim # number of dimensions (called axes in numpy)
In [ ]:
A.shape # size of the dimensions as a tuple
In [ ]:
A.reshape((4,1)).shape # a column vector

Definitions of dimensions¶

In [ ]:
A = np.array([1,2,3,4]).reshape(4,1)
In [ ]:
A[0]
In [ ]:
A[0,0]

Initializing numpy arrays¶

In [ ]:
# can initialize an array with a list, or list of lists (or list of lists of lists, etc)
M = np.array([[1,2,3], [4,5,6.0]])
print(M.dtype, M.shape)
In [ ]:
# if know the size, but not the data, can initialize to zeros:
Z = np.zeros((10,10))
# or ones
O = np.ones((5,10))
# or identity
I = np.identity(3) # this makes a 3x3 square identity matrix
In [ ]:
print(Z.dtype) # note, default type is floating point
In [ ]:
Z = np.zeros((10,10),np.int64) # can change type
print(Z.dtype)

numpy arrays behave like vectors¶

In [ ]:
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
x + y
In [ ]:
z = np.array([1, 1, 1, 1])
x + z

More math with arrays¶

By default, mathematical operations on numpy arrays with the same shape are performed element-wise

Vector/matrix operations (inner product, etc.) can be accessed via other numpy functions

In [ ]:
x = np.array([1, 2, 3])
3 * x
In [ ]:
x * x
In [ ]:
y = np.array([2, 2, 2])
x**y
In [ ]:
x/y

Indexing and slicing¶

numpy arrays can be indexed and sliced a lot like python lists, but take tuples of values to reference each dimension

In [ ]:
M = np.array([[0,1,2],[3,4,5]])
M
In [ ]:
print(M[1,1])  # indexing
print(M[0,-1]) # last item of first row
In [ ]:
print(M[0,1:]) # can have slices - all but first column of first row
In [ ]:
print(M[1], M[1,:]) # missing indices are treated as complete slices

What is M[1,1]?¶

In [ ]:
M = [[0,1,2],[3,4,5]]
In [ ]:
M[1, 1]

Advanced slicing: integers¶

numpy arrays support advanced indexing by arrays of integers or booleans:

In [ ]:
A = np.array([0,1,4,9,16,25])
In [ ]:
print(A[[2,5]]) # choose just indices 2 and 5

Advanced slicing: boolean¶

Boolean numpy arrays can be used to select elements

In [ ]:
b = A > 4
print(b)
In [ ]:
print(A[b])

Slicing assignment¶

In [ ]:
print("b =",b)
A[b] = 0
In [ ]:
print(A)

What is the new value of S?¶

In [ ]:
S = np.array(['a','b','c','b','a'])
S[S != 'a'] = 'z'
In [ ]:
S

Array views vs. copies¶

  • A numpy array object has a pointer to a dense block of memory that stores the data of the array
  • Basic slices are just views of this data - they are not a new copy
  • Binding the same object to different variables will not create a copy
  • Advanced slices will create a copy if bound to a new variable - these are cases where the result may contain elements that are not contiguous in the original array
  • Advice: if you want to define a new, independent numpy array, do so explicitly

Views¶

In [ ]:
A = np.array([[0,1,2],[3,4,5],[6,7,8]])
In [ ]:
B = A   # A and B reference the *same* object
A is B
In [ ]:
B[0,0] = 1000
A

Sliced views¶

In [ ]:
row = A[1,:]
row
In [ ]:
row[2] = 5000
A

Explicit copy¶

In [ ]:
newMat = A.copy() # this will actually copy the data
newMat[0,0] = 0
A
In [ ]:
newMat

Python also has a deepcopy function for containers that have references inside -- advanced usage

Advanced slices copy¶

In [ ]:
A = np.array([[0,1,2],[3,4,5],[6,7,8]])
B = A[A > 4]
B
In [ ]:
B[:] = -1
B
In [ ]:
A

however...

In [ ]:
A[A > 4] = -1
A

What is the value of A after this function call?¶

In [ ]:
def z(M):
    M[:] = 0
A = np.array([1,2,3])
z(A)
A

Functions on arrays¶

numpy includes a number of standard functions that will work on arrays (or data types that can be converted into arrays)

In [ ]:
A = [1,2,3,4]
np.mean(A)
In [ ]:
np.sum(A)
In [ ]:
np.sin(A)

Axes¶

Most aggregation operations take an axis parameter that limits the operation to a specific direction in the array

  • axis 0: across rows (apply operation to individual columns)
  • axis 1: across columns (apply operation to individual rows)
In [ ]:
b = np.arange(12).reshape(3,4)
b
In [ ]:
np.sum(b)
In [ ]:
np.sum(b, axis=0)
In [ ]:
np.sum(b, axis=1)

Loading data¶

genfromtxt (and the simpler loadtxt) can read in delimited files

In [ ]:
np.genfromtxt('../files/Spellman.csv')

The default delimiter is whitespace which will not work with a csv

In [ ]:
np.genfromtxt('../files/Spellman.csv', delimiter=',')

Loading data¶

Recall that numpy arrays are dense, uniformly typed arrays. Can't mix a gene name (string) with expression values (float).

In [ ]:
strdata = np.genfromtxt('../files/Spellman.csv', dtype=str, delimiter=',')
strdata
In [ ]:
header = strdata[0,1:].astype(int)
genes = strdata[1:,0]
values = strdata[1:,1:].astype(float)
In [ ]:
len(strdata), len(strdata[0])
In [ ]:
genes.shape

Data normalization¶

Q1: How would you rescale your data to range from 0 to 1?

(values-values.min())/(values.max()-values.min())

Q2: How would you rescale your data to have zero mean and unit standard deviation?

np.std((values-values.mean())/values.std())

Activity: Expression data¶

https://MSCBIO2025-2025.github.io/files/Spellman.csv

  • Read this data into a numpy array
  • Plot a histogram of the expression values for the first time point
  • Plot a histogram of the expression values for the last time point
  • Plot a histogram of the average expression value for the genes across all time points
  • Plot the average expression value (across all genes) at each time point as a line graph
  • Plot two series of average expression values: one for all genes where the first value is positive and the other for all genes where the first value is negative
In [ ]:
f = open('../files/Spellman.csv')
lines = f.readlines()
print(lines[0])
print(lines[1])
In [ ]:
import numpy as np
import matplotlib.pyplot as plt
times = np.array(lines[0].replace('\n', '').split(',')[1:], float)
exps = np.array(lines[1].replace('\n', '').split(',')[1:], float)
plt.plot(times, exps);
In [ ]:
import matplotlib.pyplot as plt
#bins = [-3,-2,-1,0,1,2,3]
#bins = np.linspace(-3,3,100)
plt.hist(values[:,0],bins=100);
In [ ]:
plt.hist(values[:,-1],bins=100);
In [ ]:
bins = np.linspace(-3,3,100)
plt.hist(values[:,0],bins=bins, alpha=0.5,label="ts-40")
plt.hist(values[:,-1],bins=100,alpha=0.5,label="ts-260")
plt.legend(loc="best");
plt.xlabel("Expression", size=14)
plt.ylabel("Number of Instances", size=14)
In [ ]:
plt.hist(values.mean(axis=1),bins=100);
In [ ]:
plt.plot(header,values.mean(axis=0))
plt.xlabel("Time",size=14)
plt.ylabel("Avg. Expression",size=14);
In [ ]:
plt.plot(header,(values[values[:,0]>0]).mean(axis=0),label="positive")
plt.plot(header,(values[values[:,0]<0]).mean(axis=0),label="negative");
plt.xlabel("Time",size=14)
plt.ylabel("Avg. Expression",size=14)
plt.legend()

For next time¶

Modeling simple differential equations in Python